| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- react
- 개발자취업부트캠프
- useRef
- 공식문서
- 내일배움카드
- CSS
- 이벤트
- 프론트엔드
- 리액트
- 개발 공부
- useMemo
- 자료구조
- next.js
- MegabyteSchool
- styled-components
- 프로그래머스
- 메가바이트스쿨
- 패스트캠퍼스
- 자바스크립트
- TypeScript
- 입문
- JavaScript
- 알고리즘
- 비전공자
- 모던 딥 다이브 자바스크립트
- 국비지원교육
- 코딩테스트
- Github
- 모던 자바스크립트 딥 다이브
- GIT
- Today
- Total
개발 기록 남기기✍️
[알고리즘] 깊이 우선 탐색(DFS) 본문
📊 그래프
그래프에서 탐색은 크게 DFS와 BFS 두 가지로 나뉜다.
그래프의 가장 기본적인 정의는 정점(vertex)과 간선(edge)의 집합이다.
간선은 두 정점을 이어주는 역할을 하며, 자기 자신을 이을 수도 있고, 간선에 방향이 있기도 하고 없기도 하며, 가중치가 있기도 하고 없기도 하는 등 아주 다양한 형태의 그래프가 있다.

정점의 집합을 보통 대문자 V로 표현한다. 여기서는 V = {1,2,3,4,5,6}이다. 간선의 집합을 보통 대문자 E로 표현한다. 간선은 양 끝점의 정점 쌍으로 표현한다. 여기서는 E = {(1,2), (1,5), (2,3), (2,5), (3,4), (4,5), (4,6)}이다. V와 E는 집합이므로 그 크기 또한 집합에 절댓값 기호를 씌워서 표현할 수 있다. 여기서는 |V| = 6, |E| = 7이다.
또한 각 정점(노드)마다 차수(degree)가 존재하는데 이는 그 정점과 이어진 간선의 개수를 말한다. 1번 정점의 차수는 2,5번 정점의 차수는 3이다.
그래프의 종류는 간선의 형태에 따라서 이분할 수 있으며 그 형태도 다양하다.
그래프 종류
📍무방향 그래프, 방향 그래프
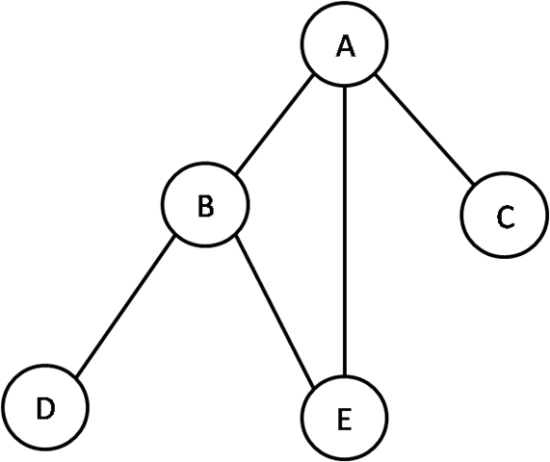
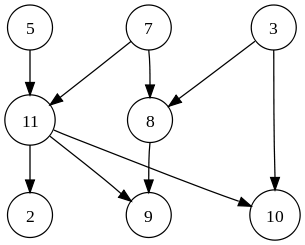
무방향 그래프는 간선의 방향이 없는 것을 의미하며 방향 그래프는 간선의 방향이 있는 것을 의미한다. 간선의 방향이 없다는 것은 어느 방향으로든 이동할 수 있다는 것이고, 방향이 있다는 것은 화살표 방향으로만 이동할 수 있다는 의미를 강하게 가진다.
무방향 그래프에서는 인접한다(adjacent)는 표현이 있는데 이는 정점 A에서 간선 하나를 거쳐서 정점 B로 이동할 수 있을 때 A와 B가 인접하다는 뜻이다.
방향 그래프에서도 이런 표현이 가능하기는 하지만, 무방향 그래프에서는 양방향으로 성립하는 반면, 방향 그래프에서는 한쪽으로만 성립할 수 있다.
방향 그래프는 차수를 양분할 수 있는데 indegree는 들어오는 간선의 수, outdegree는 나가는 간선의 수이다. 또한 방향 그래프에서 많이 사용되는 개념 중 cycle이라는 것이 있는데, 간선을 따라가다 시작한 정점으로 돌아오는 경로를 말한다.
📍가중치 그래프
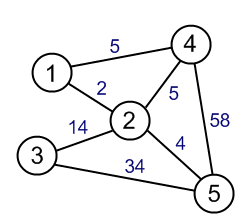
가중치 그래프는 간선들에 가중치가 있다. 이는 비용(weight)일 수도 있고, 두 정점 사이의 거리(distance)를 의미하기도 하며, 때로는 한번에 이동 가능한 최대 양인 대역폭(bandwidth)를 의미하기도 한다. 방향성을 가지면서 가중치 그래프일 수도 있다.
📍멀티 그래프

멀티 그래프는 똑같은 정점 쌍 사이에 간선이 여러 개일 수 있다. 정점의 입장에서 반대쪽 정점이 같은 간선이 여러 개일 수도 있고, 자기 자신으로 돌아오는 간선도 존재한다.
🔍 깊이 우선 탐색
깊이 우선 탐색이란 루트 노드(혹은 다른 임의의 노드)에서 시작해서 다음 분기로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법이다.
넓게 탐색하기 전에 깊게 탐색하는 것으로, 모든 노드를 방문하고자 하는 경우에 이 방법을 선택한다. 깊이 우선 탐색이 너비 우선 탐색보다 더 간단하지만, 단순 검색 속도 자체는 너비 우선 탐색에 비해서 느리다는 단점이 있다.
깊이 우선 탐색은 자기 자신을 호출하는 순환 알고리즘의 형태를가지고 있다. 전위 순회를 포함한 다른 형태의 트리 순회는 모두 DFS의 한 종류이다. 이 알고리즘을 구현할 때 가장 큰 차이점은, 그래프 탐색의 경우 어떤 노드를 방문했었는지 여부를 반드시 검사해야 한다는 것이다. 이를 검사하지 않을 경우 무한 루프에 빠질 위험이 있다.
📍깊이 우선 탐색 순서

- a 노드(시작 노드)를 방문한다.
- 방문한 노드는 방문했다고 표시한다.
- a와 인접한 노드들을 차례로 순회한다.
- a와 인접한 노드가 없다면 종료한다.
- a와 이웃한 노드 b를 방문했다면, a와 인접한 또 다른 노드를 방문하기 전에 b의 이웃 노드들을 전부 방문해야 한다.
- b를 시작 정점으로 DFS를 다시 시작하여 b의 이웃 노드들을 방문한다.
- b의 분기를 전부 완벽하게 탐색했다면 다시 a에 인접한 정점들 중에서 아직 방문이 안 된 정점을 찾는다.
- 즉, b의 분기를 전부 완벽하게 탐색한 뒤에야 a의 다른 이웃 노드를 방문할 수 있다는 뜻이다.
- 아직 방문이 안 된 정점이 없으면 종료한다.
- 있으면 다시 그 정점을 시작 정점으로 DFS를 시작한다.
💻 예시 코드
[재귀형 코드]
// 순회를 시작할 정점 노드를 인수로 받는다.
depthFirstRecursive(start) {
// 결과를 저장할 빈 배열 result를 만든다(마지막에 이것을 return할 것이다)
const result = [];
// 방문한 정점들를 기록할 빈 객체 visted를 만든다.
const visited = {};
const { adjacencyList } = this;
// 재귀를 도울 헬퍼 함수를 정의하며, start를 인수로 받아 즉시 실행한다.
(function dfs(vertex) {
// 만약 정점이 비었다면 return 한다.
if (!vertex) return null;
// 방문한 정점을 visited 객체에 true로 기록한다.
visited[vertex] = true;
// 방문한 정점을 result 배열에 추가한다.
result.push(vertex);
// 방금 방문한 정점과 간선으로 이어진 노드 중에서 아직 방문하지 않은 노드들에 대하여
// 본 헬퍼 함수를 재귀한다.
adjacencyList[vertex].forEach(neighbor => {
if (!visited[neighbor]) {
return dfs(neighbor);
}
});
})(start);
// 순회한 정점이 순서대로 담긴 배열 result를 return한다.
return result;
}
[순환형 코드]
depthFirstIterative(start) {
// stack 배열을 정의하고, start 노드를 추가한다.stack은 반복문에서 조건으로 사용할 것이다.
const stack = [start];
// 결과를 저장할 빈 배열 result를 만든다(마지막에 이것을 return할 것이다)
const result = [];
// 방문한 정점들를 기록할 빈 객체 visted를 만든다.
const visited = {};
let currentVertex;
// visited 객체에 start 노드는 방문했음을 기록한다.
visited[start] = true;
// stack이 비어 있지 않은 한, 무한 루프를 돌린다.
while (stack.length) {
// 여기서는 pop을 이용하여 간선 배열의 끝에서부터 정점을 꺼내어 방문한다.
// stack에서 가장 최근에 들어온 노드를 하나 꺼내어(pop), currentVertex 변수에 할당한다.
currentVertex = stack.pop();
// 지금 방문한 정점을 result 배열의 마지막에 추가(push)한다.
result.push(currentVertex);
// 지금 방문한 정점과 간선으로 이어진 정점 중
this.adjacencyList[currentVertex].forEach(neighbor => {
// 아직 방문하지 않은 이웃 정점에 대하여
if (!visited[neighbor]) {
// visited 객체에 이제 방문했음을 기록하고
visited[neighbor] = true;
// stack 배열(while문 종료 조건이었죠~)에 push한다.
// stack에는 이제 start 정점은 없고 그 다음에 방문한 정점 하나가 있게 되며, 다시 while문을 돈다.
stack.push(neighbor);
}
});
}
// 반복문이 다 종료된 후 result를 반환한다.
return result;
}
DFS는 그래프(정점의 수 : N, 간선의 수 : E)의 모든 간선을 조회하기 때문에 인접 리스트로 표현된 그래프는 O(N + E)를 갖는다. 한 번 방문한 정점은 다시 방문하지 않으며, 한 정점에서 다음으로 방문할 노드들을 순회하는 횟수가 그 정점의 차수와 같기 때문이다.
만약 인접 리스트가 아닌 인접 행렬로 표현된 그래프라면 다음에 방문할 정점을 찾을 때 모든 정점을 순회하며 정점이 이어져 있는지를 확인해야 하므로 O(N^2)의 시간 복잡도를 가진다.
'기초 지식 > CS' 카테고리의 다른 글
| [알고리즘] 너비 우선 탐색(BFS) (0) | 2023.07.07 |
|---|---|
| [알고리즘] 큐 (Queue), 덱(Dequeue) (0) | 2023.07.05 |
| [알고리즘] 기본 정렬 알고리즘 (0) | 2023.07.03 |



