| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 메가바이트스쿨
- 코딩테스트
- 입문
- 자료구조
- 모던 자바스크립트 딥 다이브
- CSS
- 패스트캠퍼스
- 국비지원교육
- next.js
- 자바스크립트
- 내일배움카드
- react
- 개발 공부
- 프론트엔드
- 알고리즘
- useMemo
- Github
- useRef
- TypeScript
- 리액트
- 모던 딥 다이브 자바스크립트
- 프로그래머스
- GIT
- JavaScript
- 개발자취업부트캠프
- styled-components
- 비전공자
- 이벤트
- MegabyteSchool
- 공식문서
- Today
- Total
개발 기록 남기기✍️
[알고리즘] 기본 정렬 알고리즘 본문
🧐 정렬 알고리즘
정렬 알고리즘은 n개의 숫자가 입력으로 주어졌을 때, 이를 사용자가 지정한 기준에 맞게 정렬하여 출력하는 알고리즘이다.
예를 들어 n개의 숫자가 저장되어 있는 배열을 오름차순의 조건으로 작성하여 입력하면 오름차순으로 정렬된 배열을 출력으로 구할 수 있다.
정렬 방법에 따라 각각의 수행시간도 천차 만별이다.
🔍 1. 선택 정렬(Selection Sort)

선택 정렬은 현재 위치에 들어갈 값을 찾아 정렬하는 배열이다. 현재 위치에 저장될 값의 크기가 작냐 크냐에 따라 최소 선택 정렬(Min-Selection Sort)와 최대 선택 정렬(Max-Selection Sort)로 구분할 수 있다. 최소 선택 정렬은 오름차순으로 정렬될 것이고, 최대 선택 정렬은 내림차순으로 정렬될 것이다.
📌 선택 정렬의 기본 로직
- 정렬되지 않은 인덱스의 맨 앞에서부터, 이를 포함한 그 이후의 배열값 중 가장 작은 값을 찾아간다.
- 가장 작은 값을 찾으면 그 값을 현재 인덱스의 값과 바꿔준다.
- 다음 인덱스에서 위 과정을 반복해준다.
이 정렬 알고리즘은 n-1, n-2, ... , 1개씩 비교를 반복한다. 배열이 어떻게 되어있던지 간에 전체 비교를 진행하므로 시간복잡도는 O(n^2)이다. 공간 복잡도는 단 하나의 배열에서만 진행하므로 O(n)이다.
const selectionSort = (array) => {
for(let i = 0; i < array.length; i++){
let minIdx = i;
for (let j = i + 1; j < array.length; j++){
if(array[minIdx] > arr[j]) {
minIdx = j
}
}
if(minIdx !== i) {
[array[i], array[minIdx]] = [array[minIdx], arr[i]]
}
}
return array
}🌱 장점
- 실제 사람들이 직접 정렬한다고 할 때 진행하는 방식과 가장 유사하다.
- 알고리즘 구현 난이도가 굉장히 낮고, 단순한 정렬 알고리즘이다.
- 제자리 정렬(In-place sort)의 특징을 가지고 있기 때문에, 주어진 공간 외에 추가적인 메모리를 필요로 하지 않는다. 메모리가 제한적인 상황에서 메모리를 추가적으로 할당해서 사용하는 상황에 한해서는 추가적인 메모리를 요하는 정렬 알고리즘에 비해 성능 상의 이점이 있을 가능성이 있다.
🌱 단점
- 현재 값이 최솟값임에도 불구하고 최솟값을 찾기 위한 순회 과정을 진행한다. (불필요한 순회과정이 포함되어 있다.)
- 최솟값을 찾는 횟수가 정해져있다. (n-1, n-2, ..., 1)
- O(n^2)의 시간복잡도를 가진만큼 퍼포먼스 측면에서 좋지 않다.
- 불안정 정렬(unstable sort)로써 동일한 값에 대해 기존의 순서가 뒤바뀔 수 있는 정렬 방식이다.
🔍 2. 삽입 정렬(Insertion Sort)

삽입 정렬은 현재 위치에서 그 이하의 배열들을 비교하여 자신이 들어갈 위치를 찾아 그 위치에 삽입하는 배열 알고리즘이다.
📌 삽입 정렬의 기본 로직
- 삽입 정렬은 두 번째 인덱스부터 시작한다. 현재 인덱스는 별도의 변수에 저장해주고, 비교 인덱스를 현재 인덱스 -1로 잡는다.
- 별도로 저장해 둔 삽입을 위한 변수와 비교 인덱스의 배열 값을 비교한다.
- 삽입 변수의 값이 더 작으면 현재 인덱스로 비교 인덱스의 값을 저장해주고 비교 인덱스를 -1하여 비교를 반복한다.
- 만약 삽입 변수가 더 크면, 비교 인덱스 + 1에 삽입 변수를 저장한다.
삽입 정렬 또한 최악의 경우(역으로 정렬되어있을 경우)엔 n-1, n-2, ..., 1개씩 비교를 반복하여 시간복잡도는 O(n^2)이지만, 이미 정렬되어 있는 경우에는 한번씩 밖에 비교를 하지 않아 시간 복잡도는 O(n)이다.
하지만 상한을 기준으로 하는 Big-O 표기법은 최악의 경우를 기준으로 평가하므로 삽입 정렬의 시간복잡도는 O(n^2)이다.
공간복잡도는 단 하나의 배열에서만 진행하므로 O(n)이다.
const insertionSort = (arr) => {
for (let i = 1; i < arr.length; i++) {
let currentVal = arr[i];
let j;
for (j = i - 1; j >= 0 && arr[j] > currentVal; j--) {
arr[j + 1] = arr[j];
}
arr[j + 1] = currentVal;
}
return arr;
}🌱 장점
- 알고리즘이 단순하다.
- 추가적인 메모리 소비가 적다.
- 거의 정렬된 경우 매우 효율적이고 최선의 경우 O(n)의 시간복잡도를 갖는다.
- 안정 정렬이 가능하다.
🌱 단점
- 비교적 많은 수들의 이동을 포함하며 비교할 수가 많고 크기가 클 경우에 적합하지 않다.
- 최악의 경우 O(n^2)의 시간복잡도를 갖는다.
- 데이터의 상태에 따라서 성능 편차가 매우 크다.
🔍 3. 버블 정렬(Bubble Sort)
버블 정렬은 매번 연속된 두 개 인덱스를 비교하여, 정한 기준의 값을 뒤로 넘겨 정렬하는 방법이다. 오름차순으로 정렬하고자 할 경우, 비교 시마다 큰 값이 뒤로 이동하여, 1바퀴 돌 시 가장 큰 값이 맨 뒤에 저장된다. 맨 마지막에는 비교하는 수들 중 가장 큰 값이 저장되기 때문에, (전체 배열의 크기 - 현재까지 순환한 바퀴 수)만큼만 반복해 주면 된다.
📌 버블 정렬의 기본 로직
- 삽입 정렬은 두 번째 인덱스부터 시작한다. 현재 인덱스 값과, 바로 이전의 인덱스 값을 비교한다.
- 만약 이전 인덱스가 더 크면, 현재 인덱스와 바꿔준다.
- 현재 인덱스가 더 크면, 교환하지 않고 다음 두 연속된 배열값을 비교한다.
- 이를 (전체 배열의 크기 - 현재까지 순환한 바퀴 수)만큼 반복한다.
버블 정렬은 1부터 비교를 시작하여 n-1, n-2, ..., 1개씩 비교를 반복하며, 선택 정렬과 같이 배열이 어떻게 되어있던지 간에 전체 비교를 진행하므로 시간복잡도는 O(n^2)이다. 공간 복잡도도 이 또한 단 하나의 배열에서만 진행하므로 O(n)이다.
const bubbleSort = (array) => {
for(let i=0; i < array.length; i++){
for(let j=0; j < array.length - (i+1); j++){
if(array[j] > array[j + 1]){
[array[j], array[j+1]] = [array[j+1], array[j]]
}
}
}
return array
}
🌱 장점
- 단순하게 인접한 두 요소를 비교하기 때문에 구현이 굉장히 단순하다.
🌱 단점
- 수행 시간이 굉장히 오래 걸린다.
- 불필요한 교환이 이뤄질 가능성이 크다. (최종 단계에서는 현재 위치가 맞음에도 불구하고, 인접한 두 요소 간의 비교에 의해 위치가 변경된다.)
🔍 4. 병합 정렬(Merge Sort)
병합 정렬은 분할 정복(Divide and conquer) 방식으로 설계된 알고리즘이다. 분할 정복은 큰 문제를 반으로 쪼개 문제를 해결해 나가는 방식으로, 분할은 배열의 크기가 1보다 작거나 같을 때까지 반복한다.
입력으로 하나의 배열을 받고, 연산 중에 두 개의 배열로 계속 쪼개나간 뒤 합치면서 정렬해 최후에는 하나의 정렬을 출력한다.
병합은 두 개의 배열을 비교하여 기준에 맞는 값을 다른 배열에 저장해나간다. 오름차준의 경우 배열 A, 배열 B를 비교하여 A에 있는 값이 더 작다면 새 배열에 저장해주고, A 인덱스를 증가시킨 후 A,B의 반복을 진행한다. 이는 A는 B 중 하나가 모든 배열값들을 새 배열에 저장할 때까지 반복하며, 전부 다 저장하지 못한 배열의 값들은 모두 새 배열의 값에 저장해준다.
📌 분할 과정의 기본 로직
- 현재 배열을 반으로 쪼갠다. 배열의 시작 위치와 종료 위치를 입력받아 둘을 더한 후 2를 나눠 그 위치를 기준으로 나눈다.
- 이를 쪼갠 배열의 크기가 0이거나 1일 때까지 반복한다.
📌 병합 정렬의 기본 로직
- 두 배열 A, B의 크기를 비교한다. 각각의 배열의 현재 인덱스를 i,j로 가정한다.
- i에는 A 배열의 시작 인덱스를 저장하고, j에는 B배열의 시작 주소를 저장한다.
- A[i]와 B[j]를 비교한다. 오름차순의 경우 이중에 작은 값을 새 배열 C에 저장한다. A[i]가 더 컸다면 A[i]의 값을 배열 C에 저장해주고, i의 값을 하나 증가시켜준다.
- 이를 i나 j 둘 중 하나가 각자 배열의 끝에 도달할 때까지 반복한다.
- 끝까지 저장을 못한 배열의 값을 순서대로 전부 다 C에 저장한다.
- C 배열을 원래의 배열에 저장해준다.
병합 과정은 두 배열 A,B를 정렬하기 때문에 A배열의 크기를 N1, B배열의 크기를 N2라고 할 경우 O(n1+n2)와 같다. 배열 A와 배열 B는 하나의 배열을 나눈 배열들이기 때문에 전체 배열의 길이가 N이라고 할 경우 N = N1 + N2 이므로 O(n)이라고 할 수 있다.
분할 과정은 logN 만큼 일어나는데, 크기가 N인 배열을 분할 하면 분할 과정은 매번 반씩 감소하므로 logN만큼 반복해야 크기가 1인 배열로 분할할 수 있다.
각 분할 별로 합병을 진행하므로, 병합 정렬의 시간 복잡도는 O(NlogN)이다. 사용하는 공간은 정렬을 위한 배열을 하나 더 생성하므로 2N개 사용한다.
function merge(left, right) {
const sortedArr = [];
while (left.length && right.length) {
//left[0]이 더작을 경우 같을때는 누가 먼저 들어가도 상관X
if (left[0] <= right[0]) {
sortedArr.push(left.shift());
} else {
sortedArr.push(right.shift());
}
}
//left,right 둘 중 하나는 요소가 남아있기 때문에 sortedArr 뒤에 붙여서 출력
//비어있으면 spread Syntax에도 아무것도 없기 때문에 그냥 다 붙여준다.
return [...sortedArr, ...left, ...right];
}
function mergeSort(arr) {
if (arr.length === 1) return arr;
const boundary = Math.ceil(arr.length / 2);
//slice로 해주기 때문에 원본 arr은 손상 없다.
const left = arr.slice(0, boundary);
const right = arr.slice(boundary);
//요소가 1개 일 때까지 재귀를 실행해 요소가 1개일 때 두 left,right부터
//차근차근 merge(정렬해서 합치기)해주면 된다.
return merge(mergeSort(left), mergeSort(right));
}🌱 장점
- 원본 배열을 절반씩 분할해가면서 정렬하는 정렬법으로써 분할하는 과정에서 logN만큼의 시간이 소요된다.
- 기준값을 설정하는 과정없이 무조건 절반으로 분할하기에 기준값에 따라 성능이 달라지는 경우가 없다. 따라서 항상 O(NlogN)이라는 시간복잡도를 가지게 된다.
🌱 단점
- 병합정렬은 임시 배열에 원본 맵을 계속해서 옮겨주며 정렬을 하는 방식이기 추가적인 메모리가 필요하다.
🔍 5. 퀵 정렬(Quick Sort)
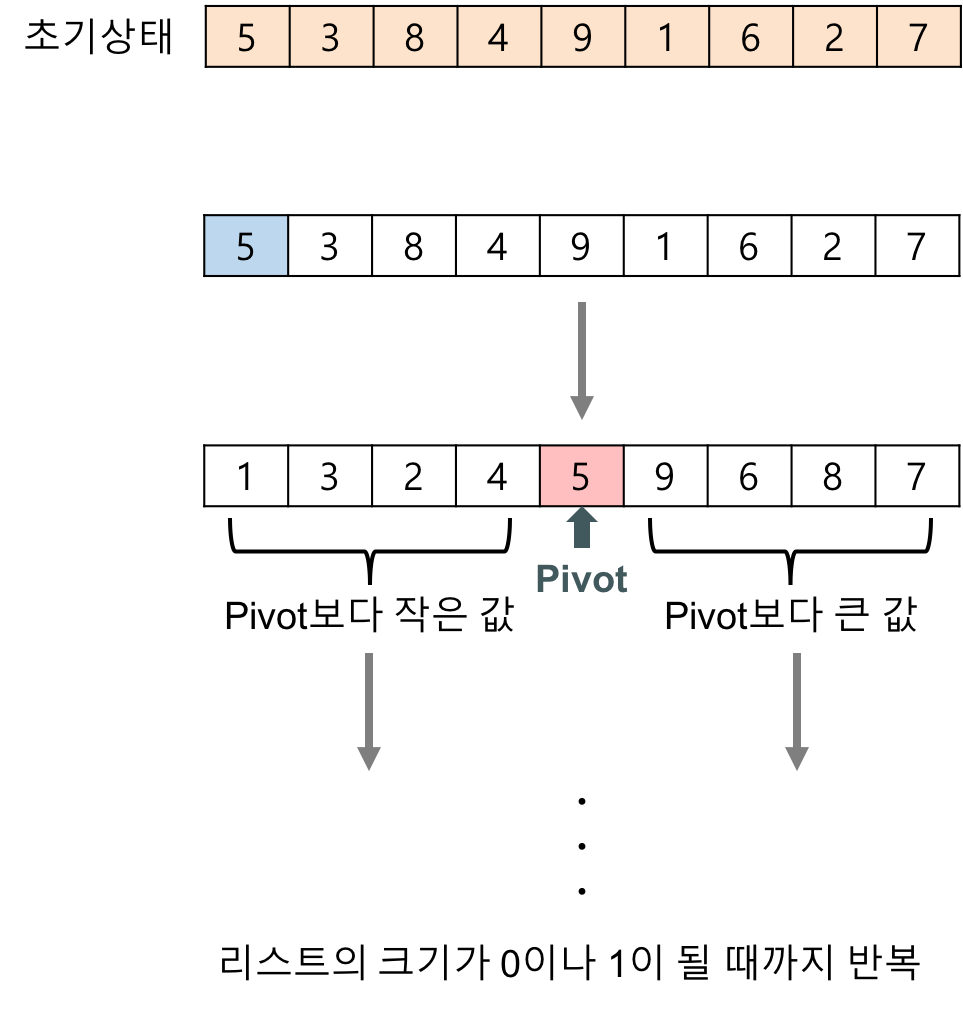
퀵 정렬 또한 분할 정복을 이용하여 정렬을 수행하는 알고리즘이다. 피벗 포인트(pivot point)라고 기준이 되는 값을 하나 설정하는데, 이 값을 기준으로 작은 값은 왼쪽, 큰 값은 오른쪽으로 옮기는 방식으로 정렬을 진행한다. 이를 반복하여 분할된 배열의 크기가 1이 되면 배열이 모두 정렬된 것이다.
📌 퀵 정렬의 기본 로직
- 피벗 포인트로 잡을 배열의 값 하나를 정한다. 보통 맨 앞이나 맨 뒤, 혹은 전체 배열 값 중 중간값이나 랜덤 값으로 정한다.
- 분할을 진행하기에 앞서, 비교를 진행하기 위해 가장 왼쪽 배열의 인덱스를 저장하는 left 변수, 가장 오른쪽 배열의 인덱스를 저장한 right 변수를 생성한다.
- right부터 비교를 진행한다. 비교는 right가 left보다 클 때만 반복하며 비교한 배열 값이 피벗 포인트보다 작으면 left를 하나 증가시키고 비교를 반복한다.
- 그 다음 left부터 비교를 진행한다. 비교는 right가 left보다 클 때만 반복하며, 비교한 배열 값이 피벗 포인트보다 작으면 left를 하나 증가시키고 비교를 반복한다. 피벗 포인트보다 큰 배열 값을 찾으면 반복을 중지한다.
- left 인덱스의 값과 right 인덱스의 값을 바꿔준다.
- 3,4,5 과정을 left < right가 만족할 때까지 반복한다.
- 위 과정이 끝나면 left의 값과 피벗 포인트를 바꿔준다.
- 맨 왼쪽부터 left - 1까지, left + 1부터 맨 오른쪽으로 나눠 퀵 정렬을 반복한다.
const quickSort = function (arr) {
if (arr.length <= 1) return arr;
const pivot = arr[0];
const left = [];
const right = [];
for (let i = 1; i < arr.length; i++) {
if (arr[i] <= pivot) left.push(arr[i]);
else right.push(arr[i]);
}
const lSorted = quickSort(left);
const rSorted = quickSort(right);
return [...lSorted, pivot, ...rSorted];
};
🌱 장점
- 기준 값(Pivot)에 의한 분할을 통해 구현하는 정렬 방법으로, 분할 과정에서 logN이라는 시간이 소요되며, 전체적으로 N x logN으로 준수
🌱 단점
- 최악의 기준값을 선택할 경우 O(N^2)라는 시간복잡도를 가지게 됨
🔍 정렬 별 시간복잡도 정리

'기초 지식 > CS' 카테고리의 다른 글
| [알고리즘] 너비 우선 탐색(BFS) (0) | 2023.07.07 |
|---|---|
| [알고리즘] 깊이 우선 탐색(DFS) (0) | 2023.07.06 |
| [알고리즘] 큐 (Queue), 덱(Dequeue) (0) | 2023.07.05 |



